DROP'PI'- WHEN A NEEDLE’S QUIRKY FALL CRACKED THE CODE OF π

“Buffoon? Or Buffon?”

That’s what I wondered the first time I heard someone mention Buffon’s Needle, an experiment that, strangely enough, had something to do with finding π. 

I always thought π belonged to circles — locked away in geometry class alongside formulas we memorized and quickly forgot. But then I stumbled across something strange. A needle. Some parallel lines. And a probability experiment from the 1700s.

A French mathematician named Georges-Louis Leclerc, Comte de Buffon (1707–1788) actually figured out a way to extract π from pure chance. No circles. No radius. Just a stick, a floor, and a whole lot of randomness.

What started as a bizarre idea ended up becoming one of the earliest examples of how randomness can reveal deep truths — and how π is everywhere, even where you least expect it.

πONEERS OF PI

"The probability of success is difficult to estimate; but if we never search the chance of success is zero"

Philip Morrison

Nearly 4000 years in the past, humans looked up at the skies, down at their wheels, and into their water pots, all perfectly round. One question fascinated them:

How much longer is the edge of a circle compared to its width? 

-And so began the timeless quest to uncover the value of π (pi).

Our journey begins in ancient Babylon, around 1900 BC. The Babylonians, brilliant builders and thinkers, estimated the area of a circle by multiplying 3 with the square of its radius. That gave them π = 3. But one Babylonian tablet reveals an even sharper estimate: π ≈ 3.125.

Meanwhile, in ancient Egypt (around 1650 BC), the Rhind Papyrus showed another clever approach, leading to π ≈ 3.1605—a step closer to the truth, etched in hieroglyphs on scrolls.

Then came one of the greatest minds of the ancient world, Archimedes of Syracuse (287–212 BC).
Archimedes didn’t just guess π, he trapped it. Using polygons with many sides, drawn inside and outside a circle, he calculated their areas to pin down π between 3.1408 and 3.1429. This method, purely geometric, was revolutionary and became the gold standard for centuries.

But Archimedes wasn’t alone in the race. In India, around 500 AD, a young mathematician named Aryabhata was revolutionizing mathematics and astronomy. In his work Āryabhaṭīya, he gave a brilliant approximation of π :

“Add four to one hundred, multiply by eight, and then add sixty-two thousand.”
“Divide by twenty thousand.”

This poetic verse gives π ≈ 3.1416—astonishingly accurate for the time. Aryabhata treated π as an irrational number, something that couldn't be expressed exactly as a fraction. His work influenced generations of Indian mathematicians and showed that π was not just a number—it was a mystery worth chasing.

Far to the east, in China, Zu Chongzhi (429–501 AD) was arriving at a similar truth. He wasn’t familiar with Archimedes or Aryabhata, yet he independently calculated π as 355/113—a remarkably accurate fraction, correct to six decimal places. Historians believe he used polygons with over 24,000 sides to reach that level of precision, though his detailed method is now lost.

BUFFON ESTIMATES PI BY CHANCE!

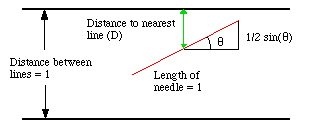
Buffon's Needle is one of the oldest problems in the field of geometrical probability. It was first stated in 1777. It involves dropping a needle on a lined sheet of paper and determining the probability of the needle crossing one of the lines on the page. The remarkable result is that the probability is directly related to the value of π.

Figure 1: Georges-Louis Leclerc, Comte de Buffon 

Mathematical interpretation

                                                                                

"Probability is nothing but common sense reduced to calculation"

Pierre Simon Laplace

Imagine a plain sheet of paper with parallel horizontal lines drawn across it, each line exactly 1 unit apart. Now, suppose you have a needle that is also 1 unit long. What happens if you drop the needle randomly onto the paper? Will it cross a line or not?

Curve 1: Graph showing how the needle aligns itself with the parallel lines when L=D=1 unit

Now we assign two random variables namely,

1. Angle (θ):

   • This is the angle the needle makes with the horizontal lines.

   • It can be anything from 0 to 180 degrees (or 0 to π radians).

2. Distance (D):

• the distance between the parallel lines on the paper. The maximum it can be is 0.5 units (half the space between lines), otherwise the needle will lie completely between the lines and won’t be able to cross one.

3. x: The maximum it can be is 0.5 units (half the space between lines), otherwise the needle will lie completely between the lines and won’t be able to cross one.

The needle will cross the line if, 

That’s because the more tilted the needle is (i.e., larger θ), the more likely it is to span across a line. At 90°, the needle is vertical and will almost always cross a line. At 0° or 180°, it's horizontal and least likely to.

Now, imagine a graph:

• Horizontal axis = angle θ from 0 to π

• Vertical axis = distance D from 0 to 0.5

If you plot the curve of D≤0.5sinθ, we obtain the following curve,

Curve 2: Probability curve for L=D=1 condition

Then everything below the curve is a situation where the needle crosses a line.

So, the probability of a hit = the area under the curve divided by the area of the full rectangle.

 Area under the curve:     

 Area of the rectangle:     

So, probability of a hit:    

This means, in the long run, about 63.66% (2/𝝅) of your drops will cross a line.

Now this is true for L=D=1, where L is the needle length and D is the line spacing.

If L and D are not equal to 1, then we consider the following condition. 

The needle crosses a line if the vertical projection of half of the needle is more than or equal to the distance to the nearest line:

where, x is the distance from the center of the needle to the nearest line.

This inequality gives us the “hit zone” in the space of possible $(x, \theta)$ values.

Now, the total area of possibilities is given by= 

Area where hits happen: 

Therefore, the probability P is given by=  

CONCLUDING NOTE:

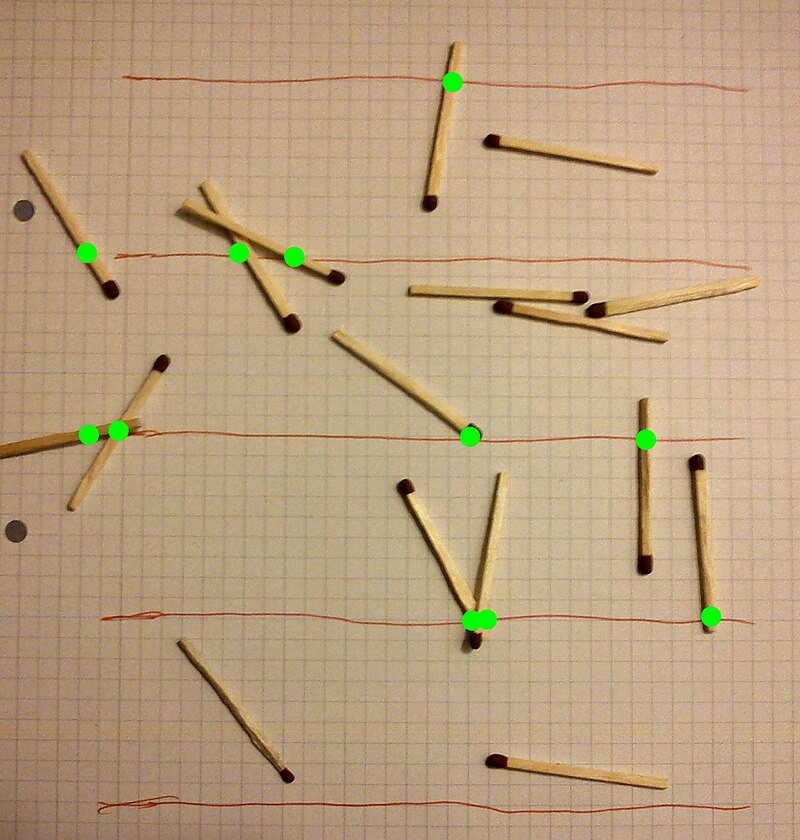
Figure 2: An experiment to find π. Matches with the length of 9 squares have been thrown 17 times between rows with the width of 9 squares. 11 of the matches have landed at random across the drawn lines marked by the green points. Substituting in Buffon Equation we obtain π≈ 3.1.

Buffon's Needle experiment offers a clever way to estimate the value of π using probability. By dropping a needle of known length onto a sheet of paper with equally spaced parallel lines, we observe how often the needle crosses a line. If we repeat this many times and count the number of hits (crossings), we can use the formula:

Here, L is the needle's length and D is the distance between the lines.

Surprisingly, through this random experiment, the constant π — usually found in circles — emerges from straight lines and probability.

The legacy of Buffon’s Needle lies in its groundbreaking role as one of the earliest examples of using randomness to solve a mathematical problem. Introduced in the 18th century by Georges-Louis Leclerc, Comte de Buffon, the experiment not only offered an unexpected way to approximate π but also laid the conceptual foundation for what would much later become the Monte Carlo method — a cornerstone of modern computational science. Buffon’s Needle beautifully illustrated that chance and probability could be harnessed to explore deep mathematical truths, bridging geometry, statistics, and physical experimentation. Its influence echoes today in fields ranging from physics and finance to artificial intelligence and climate modeling.

REFERENCES:

1. A Brief History of Pi (π)- Exploratorium

2. Buffon's Needle: An Analysis and Simulation- College of Education, Office for Mathematics, Science, and Technology Education, University of Illinois 

3. Buffon's needle problem- Wikipedia: The Free Encyclopaedia

*All the media published in this blog belongs to their original creators and 'Knowledge Through Science' does not claim any right over it.